Stress for Thick Walled Cylinders using Lamé’s Equations

Thick Walled Cylinder Stress Calculator

Summary
Thick Wall Cylindrical Hoop Stress Calculator
Thick Wall Cylindrical Radial Stress Calculator
Thick Wall Cylindrical Axial Stress Calculator

Summary

Three of the primary mechanical stresses (not to be confused with ‘principle stresses’) that can be applied to a cylindrically shaped object are:

Hoop Stress
Radial Stress
Axial Stress

If the object/vessel has walls with a thickness greater than one-tenth of the overall diameter, then these objects can be assumed to be ‘thick-walled’. The general equations to calculate the stresses are:

Hoop Stress,
(1) $\begin{align*}\sigma\x_h = A + \frac{B}{r^2}\end{align*}$
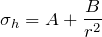
Radial Stress,
(2) $\begin{align*}\sigma\x_r = A - \frac{B}{r^2}\end{align*}$

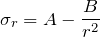
From a thick-walled cylinder, we get the boundary conditions:

$\sigma\x_r = -p\x_o$ at $r = r\x_o$ and $\sigma\x_r = -p\x_i$ at $r = r\x_i$

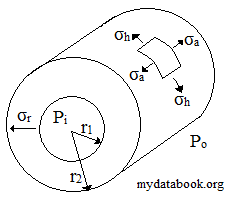
Thick Walled Cylinder

Applying these boundary conditions to the above simultaneous equations gives us the following equations for the constants A & B:

(3) $\begin{align*}A = \frac{p\x_i r\x_i ^2 - p\x_o r\x_o ^2}{r\x_o ^2 - r\x_i ^2}\end{align*}$

(4) $\begin{align*}B = \frac{(p\x_i - p\x_o) r\x_o ^2 r\x_i ^2}{r\x_o ^2 - r\x_i ^2}\end{align*}$

Finally, solving the general equations with A & B gives Lamé’s equations:

Hoop Stress,
(5) $\begin{align*}\sigma\x_h = \frac{p\x_i r\x_i ^2 - p\x_o r\x_o ^2}{r\x_o ^2 - r\x_i ^2} + \frac{(p\x_i - p\x_o) r\x_o ^2 r\x_i ^2}{(r\x_o ^2 - r\x_i ^2)r^2}\end{align*}$
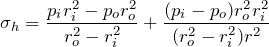
Radial Stress,
(6) $\begin{align*}\sigma\x_r = \frac{p\x_i r\x_i ^2 - p\x_o r\x_o ^2}{r\x_o ^2 - r\x_i ^2} - \frac{(p\x_i - p\x_o) r\x_o ^2 r\x_i ^2}{(r\x_o ^2 - r\x_i ^2)r^2}\end{align*}$

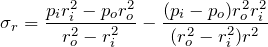
The axial stress for a closed-ended cylinder is calculated by means of the equilibrium, which reduces to:

Axial Stress,
(7) $\begin{align*}\sigma\x_a = p\x_i \frac{r\x_i ^2}{r\x_o ^2 - r\x_i ^2}\end{align*}$

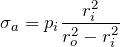
Thick Wall Cylinder Hoop Stress Calculator

Thick Wall Cylinder Radial Stress Calculator

Thick Wall Cylinder Axial Stress Calculator

Calculate the hoop stress in a thick-walled cylinder:
Formula:	$\sigma\x_h = \frac{p\x_i r\x_i ^2 - p\x_o r\x_o ^2}{r\x_o ^2 - r\x_i ^2} + \frac{(p\x_i - p\x_o) r\x_o ^2 r\x_i ^2}{(r\x_o ^2 - r\x_i ^2)r^2}$
	$\sigma\x_h$ = Hoop stress P_i = internal pressure P_o = external pressure r_i = internal radius r_o = external radius r = radius at point of interest (usually r_i or r_o)
Internal Pressure	Pa
External Pressure	Pa
Internal Radius	m
External Radius	m
Radius at Point of Interest	m

Result:	Pa

Calculate the radial stress in a thick-walled cylinder:
Formula:	$\sigma\x_r = \frac{p\x_i r\x_i ^2 - p\x_o r\x_o ^2}{r\x_o ^2 - r\x_i ^2} - \frac{(p\x_i - p\x_o) r\x_o ^2 r\x_i ^2}{(r\x_o ^2 - r\x_i ^2)r^2}$
	$\sigma\x_r$ = radial stress P_i = internal pressure P_o = external pressure r_i = internal radius r_o = external radius r = radius at point of interest (usually r_i or r_o)
Internal Pressure	Pa
External Pressure	Pa
Internal Radius	m
External Radius	m
Radius at Point of Interest	m

Result:	Pa

Calculate the axial stress in a closed-ended thick-walled cylinder:
Formula:	$\sigma\x_a = p\x_i \frac{r\x_i ^2}{r\x_o ^2 - r\x_i ^2}$
	$\sigma\x_a$ = axial stress P_i = internal pressure r_i = internal radius r_o = external radius
Internal Pressure	Pa
Internal Radius	m
External Radius	m

Result:	Pa